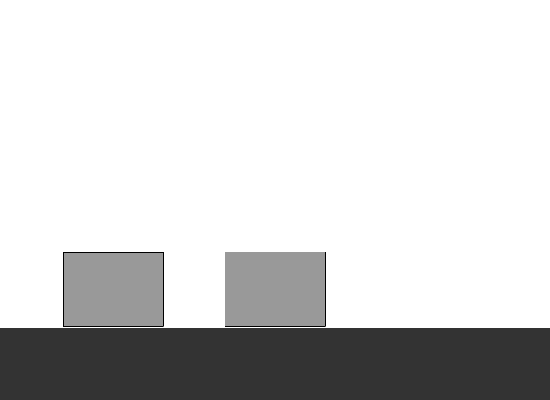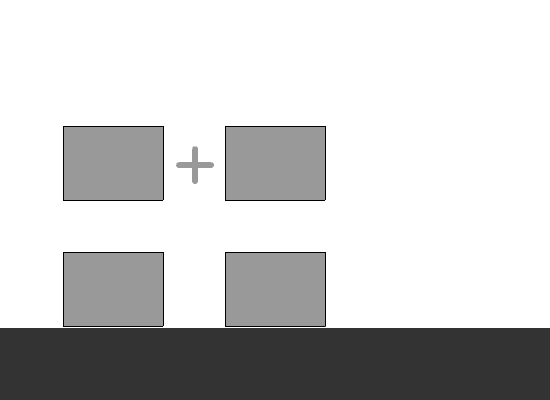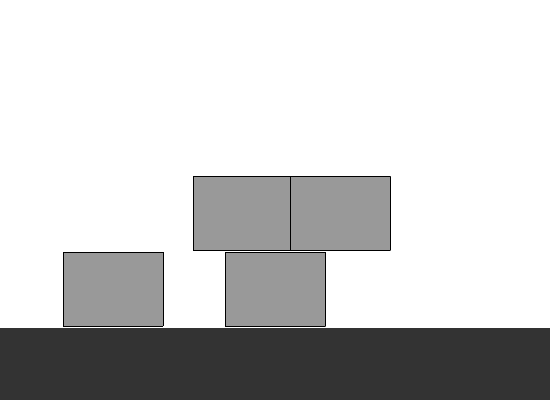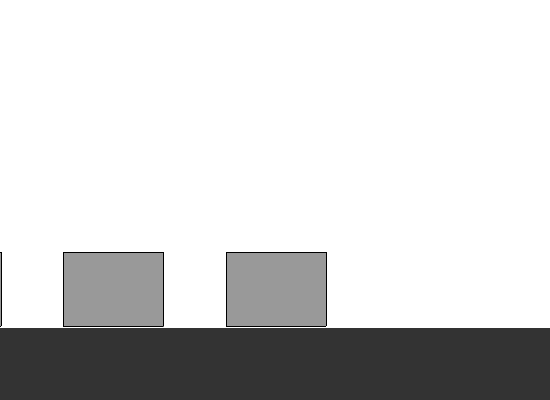Serie de Fibonacci
La belleza de la naturaleza sólo puede estar hecha o al azar o con una temible exactitud matemática. Al menos eso es lo que piensa el maestro B, quien ha quedado impresionado con la belleza de una flor. Al buscar sobre ella en internet, encontró que sigue el patrón que sigue la llamada serie de Fibonacci.
La serie de Fibonacci está creada de una manera muy particular y sencilla. Tradicionalmente empieza con el número 1. Para formar el siguiente elemento de la sucesión, es necesario sumar ese 1 a su número entero anterior (sí, el 0), ahora tendremos dos elementos en la sucesión, y para seguir fabricando más elementos, seguimos la misma regla:
En la serie de Fibonacci un elemento es la suma de sus dos elementos anteriores
Como ejemplo la serie empezaría así:
\[1, 1, 2, 3, 5, 8, 13 ...\]Ahora que la conoces
Problema
Mostrar los primeros N términos de la serie de Fibonacci.
Entrada
El entero N que expresa la cantidad de términos a mostrar.
Salida
Los primero N términos de la serie de Fibonacci separados por un espacio.
Ejemplo
Límites
Puedes considerar que \(1 \le N \le 10000\)
Solución
Razonamiento
La solución del problema, está como en muchos casos, en la descripción del mismo. Por esto, vamos a tener que concentrarnos de nuevo en la definición de la serie de Fibonacci:
En la serie de Fibonacci un elemento es la suma de sus dos elementos anteriores
Entonces, consideremos el límite de N, puede llegar a ser 10000, no podemos hacer algo como poner 10000 condicionales y mostrar manualmente cada serie según sea N. ¡No! Eso jamás se hace. Aunque N fuera máximo 3, nunca debemos hacer casos particulares. Eso resulta algo poco práctico y para nada es una solución elegante. Como programadores, debemos pensar en un método que funcione para un gran límite, que la solución sea sencilla, automática, bien comprensible, y preferentemente breve. Es decir, que sea elegante.
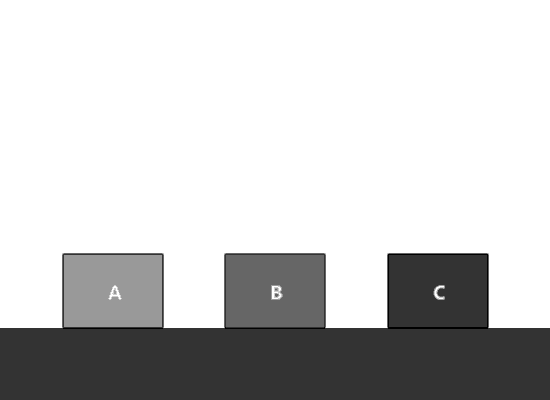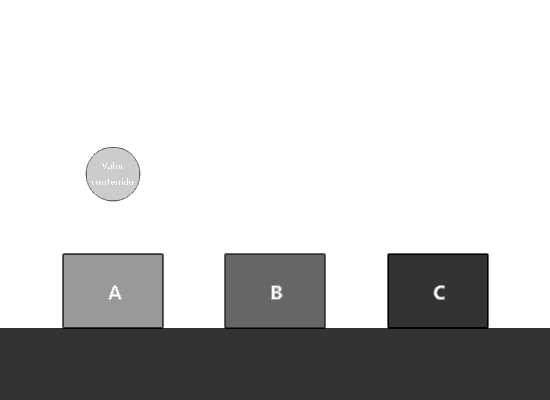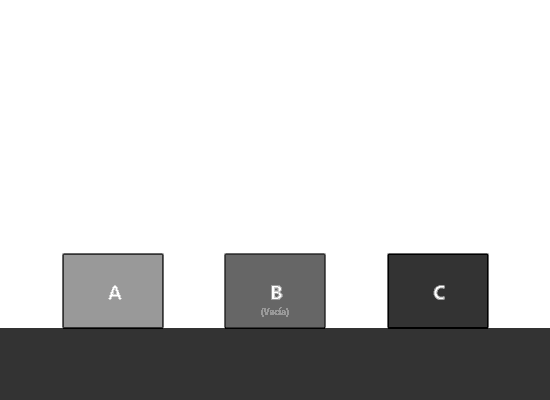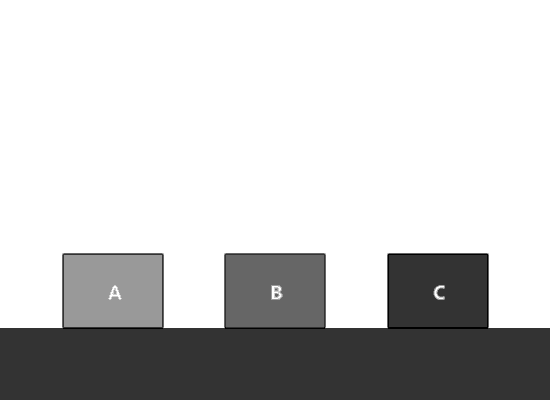
Entonces volvamos al problema. Para esto, usaremos un dibujo que nos muestre gráficamente la anterior definición.
Como podemos ver, el valor de cada término es la suma de sus dos términos anteriores. Sin embargo, y al igual que en la animación, no podemos estar creando cajas o contenedores indefinidamente. Si cada contenedor fuera una variable, tendríamos que declarar una cantidad enorme de variables, y el manejo del valor de cada una se volvería algo sumamente complicado.
Recordemos que buscamos soluciones sencillas, y elegantes. Analiza el siguiente comportamiento.
¿Logramos el mismo resultado? En efecto, el valor de cada término es igual a la suma de sus dos términos anteriores. Ahora analizamos los siguientes aspectos; ¿cuántos contenedores usamos? Sólo tres. Lo que estamos desplazando son los valores de cada contenedor. Una vez que generamos cada valor nuevo, recorremos los valores de cada variable. La variable A contiene ahora el valor de la variable B, y ésta a su vez el valor de la variable C, de esta manera, se vuelve a repetir el ciclo. Asignando el nuevo valor a C, mostrándolo y volviendo a recorrer valores. Así sólo utilizamos tres variables.
Muy bien hasta ahí, pero ¿cuál es el valor inicial de cada variable? Como sabemos, nuestra serie va más o menos 1 1 2 3 5 8 ... si queremos que primero se muestre el 1, y lo que vamos a estar mostrando es el valor de la variable C, lo que tenemos que hacer es inicializar esta variable en 1, luego mostrarla. Ahora sí pasamos el valor de B a A y después pasamos el de C a B. Para que el siguiente término nos vuelva a dar un 1, la suma de A + B tiene que ser 1, esto después del cambio que ya hicimos. Como ya le dimos a B el valor de 1 (porque era el que tenía C) necesitamos que B (cuyo valor ahora tiene A) haya sido inicializada en 0, así al sumarlas vuelva a dar 1. Después de ahí, sólo se tiene que repetir ese mismo patrón ¡y ya está!
Asegúrate de entender el funcionamiento de el principio de Fibonacci, es algo muy muy útil, que te servirá para problemas mucho más complejos.
Y la parte fácil del problema, la cantidad de términos a mostrar. Eso puede ser fácilmente controlado con un ciclo que itere desde 1 hasta N.
Pseudocódigo
Cita esta página
Include Poetry - Code. (2016, 10 de octubre). Serie de Fibonacci. Obtenido de https://www.include-poetry.com/Code/Problemas/Resueltos/C++/Serie-de-Fibonacci/