Barridos con Karel

Interpretemos como barrido el hecho de recorrer todos los espacios posibles de una determinada área. Esto resulta especialmente útil en Karel, pues la solución a muchos problemas lo requiere. Sin embargo aunque hay muchísimas formas de realizar un barrido nuestro deber es encontrar la manera óptima de hacerlo.

Problema práctico

Imagina que Karel se encuentra en la esquina inferior izquierda de un gran espacio cerrado delimitado por cuatro paredes y en cada espacio de ese cuadro hay una cantidad desconocida de zumbadores. La tarea de Karel es recoger todos los zumbadores, para después apagarse.

Como es lógico, tenemos que hacer que Karel pase por todos los espacios de esa área a la vez que tomamos el zumbador sobre el que estemos. A la acción de recorrer todos los espacios es a la que estamos llamando barrido. Así que buscaremos la manera óptima de hacerlo, donde tengamos que escribir menos y Karel lo haga lo más rápido posible.

Maneras de hacer el barrido

Consideremos las siguientes maneras de hacer un barrido

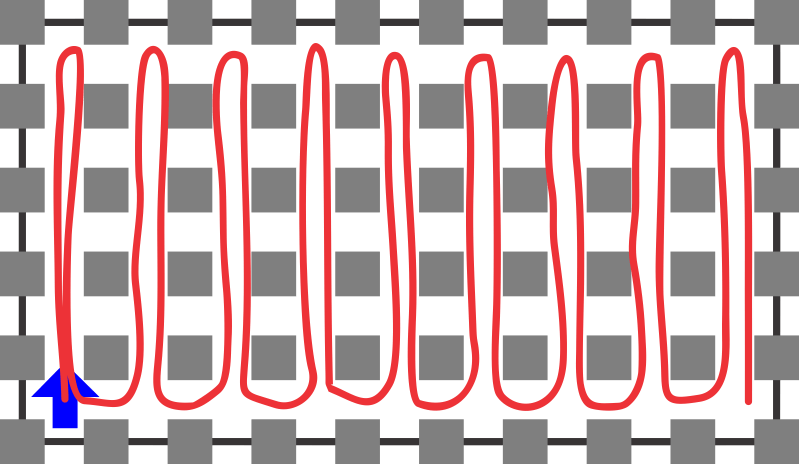
La primera como en zig zag, o también llamada comúnmente “de serpiente”.

Otra forma sería hacerlo por columnas, es decir, subir y bajar una columna y luego pasarse a la siguiente y continuar.

Otra manera puede ser en espiral, haciendo un recorrido como sigue.

Todas los métodos anteriores cumplirían con recorrer cada espacio de un área cuadrada determinada, sin embargo, tenemos que analizar cuál es la mejor manera de hacerlo. Recuerda que no sólo buscamos resolver problemas, sino hacerlo de manera óptima.

Analizando cada método

Serpiente

Para el método de serpiente, las cosas que tendríamos que considerar son las siguientes (considerando que Karel inicia en la esquina inferior izquierda orientado al norte como en los ejemplos):

• Avanzar y tomar mientras tengamos el frente libre
• Una vez que el frente esté bloqueado girar a la derecha
• Si el frente está libre entonces aún nos faltan columnas por recorrer, avanzamos una vez para ubicarnos en la nueva columna
• Girar a la derecha para estar de frente a la nueva columna con el frente libre
• Avanzar y tomar hasta que ya no tengamos el frente libre
• Ahora girar a la izquierda para pasar a la nueva columna
• Si ese frente está libre es porque aún tenemos columnas por recorrer, de ser así, avanzamos
• Nos orientamos al norte para ver de frente la columna nueva con el frente libre
• Seguimos repitiendo

Como puedes ver, hay que ir girando alternadamente a la izquierda y derecha y revisar en cada giro que el frente esté libre para poder continuar con el barrido.

Columnas

Para el método por columnas y partiendo de las mismas circunstancias que el ejemplo anterior, tendríamos que considerar lo que sigue.

• Avanzar y tomar mientras tengamos el frente libre
• Cuando ya no esté libre giramos 2 veces a la izquierda (180°) y volvemos a avanzar hasta topar
• Cuando estemos en la base de la columna de nuevo, giramos a la izquierda
• Si ese frente está libre, entonces nos faltan columnas por recorrer de ser así, avanzamos
• Giramos a la izquierda para volvernos a orientar en la nueva columna
• Seguimos repitiendo

Aquí son menos pasos y no tenemos que estar alternando direcciones de giros, por lo que los chequeos de final son menos y más concisos, sin embargo, Karel recorre dos veces cada columna, por lo que podría parecer que estamos haciendo trabajo de más.

Espiral

Para el método en espiral y de nuevo, partiendo con de las circunstancias anteriores, existen varias maneras de hacerlo, sin embargo tomaremos una de las más prácticas y sencillas.

• Tomar y avanzar mientras estemos junto a un zumbador y tengamos el frente libre
• Si nos detenemos porque el frente está bloqueado, entonces sólo tenemos que girar a la derecha y seguir
• Si nos detenemos porque ya no estamos junto a un zumbador entonces tenemos que dar media vuelta, avanzar una vez y girar a la izquierda. Es decir, volver a la casilla anterior y volvernos a ubicar.
• Tomar en consideración medidas especiales para el final del barrido, según lo que estemos haciendo

Podrán parecer menos pasos, sin embargo, este método sería mucho más complicado, si por ejemplo, el área a limpiar de zumbadores tiene huecos, o al revés, si es un campo a rellenar y ya hay zumbadores en algunos espacios. Por eso mismo, el final tendría que ser distinto según cada caso y las consideraciones variarían de complejidad también.

El método óptimo

Consideremos como el algoritmo óptimo, aquel que necesita de poco esfuerzo y líneas de código en escribirse, es fácil de entender, modificar y corregir y además tiene una ejecución bien controlada (que a cada momento sepamos qué está pasando). Otra cosa importante, es el tiempo que se tarda Karel en realizar la ejecución, recordemos que hacer chequeos también le toma un tiempo (visto a gran escala).

Podemos verlo en las descripciones generales, el algoritmo más sencillo de implementar es el método por columna, su código es más corto, rápido y fácil de escribir, se modifica fácilmente y además es muy controlado. Aunque recorremos doble las columnas, es una desventaja que vale la pena, pues por lo general el tiempo de ejecución extra que necesitamos siempre está disponible, aún con el caso más grande de espacio, es difícil que nos falte tiempo. Por lo que podemos decir que es la mejor opción.

El código

En base a la descripción general que hicimos al inicio, podemos llegar al siguiente código:

No olvides probar y asegurarte de entender el código anterior, así como implementar los otros dos barridos mencionados, puedes sacarles provecho en algunos casos, así que es también muy útil entenderlos y manejarlos.

Cita esta página

Include Poetry - Code. (2020, 4 de enero). Barridos con Karel. Obtenido de https://www.include-poetry.com/Code/Otros-temas/Karel/Barridos/